CRITERIOS DE CONGRUENCIA

CRITERIOS DE CONGRUENCIA

Se llama o denomina criterio a una norma o regla que nos permite saber la verdad, es por ello que la norma o regla que nos permite saber de manera rápida si un triángulo es congruente o no se conoce como criterio de congruencia.

Cuando se cumplen los criterios de Congruencia al comparar dos triángulos, entonces podemos concluir que existe Congruencia de Triángulos.

Los tres Criterios que se utilizan para saber si la Congruencia de Triángulos existe son:

Criterio LAL (lado, angulo, lado)

 Si dos lados y el ángulo comprendido entre ellos en un triángulo son congruentes, respectivamente, a dos lados y el ángulo comprendido entre ellos en otro triángulo, entonces los triángulos son congruentes.

Este criterio nos permite deducir la igualdad de lados entre dos triángulos cuando solo tenemos seguridad de la igualdad de uno solo de los lados y sus ángulos adyacentes coinciden.

EJEMPLO:

Los triángulos anteriores son congruentes porque cumplen con el criterio LAL.

Criterio ALA (angulo, lado, angulo)

 Si un lado y sus dos ángulos adyacentes en un triángulo son congruentes, respectivamente, a un lado y sus ángulos adyacentes en otro triángulo (adyacentes al lado), entonces los triángulos son congruentes.

Este criterio nos permite deducir la igualdad del tercer lado y del resto de los ángulos del triángulo dado, si se conoce uno de los ángulos y sus lados adyacentes. 

  

EJEMPLO:

Los triángulos anteriores son congruentes porque cumplen con el criterio ALA.

Criterio LLL (lado, lado, lado)

 Si tres lados de un triángulo son congruentes, respectivamente, a tres lados de otro triángulo, entonces los triángulos son congruentes.

Este criterio nos permite deducir la igualdad de los ángulos de los dos triángulos cuyos lados respectivos verificamos que son iguales.

EJEMPLO:

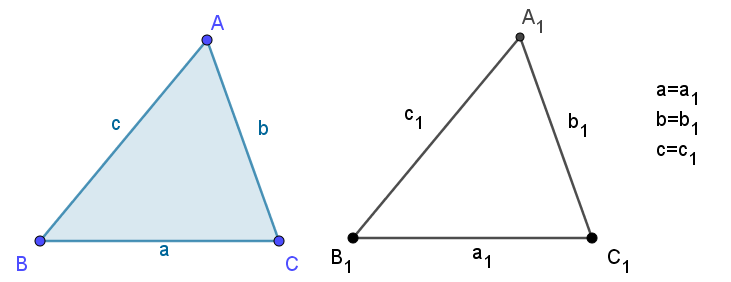
Los triángulos anteriores son congruentes porque cumplen con el criterio LLL.